A/B Testing Example (Two Mean Hypothesis Test)
A/B Testing Example (Two Mean Hypothesis Test)
by Boxplot Nov 4, 2023

A/B testing (sometimes called split testing) is comparing two versions of a web page, email newsletter, or some other digital content to see which one performs better. A company will compare two web pages by showing the two variants (let’s call them A and B) to similar visitors at the same time. Sometimes, the company is trying to see which page leads to a higher average purchase size (the amount that the average user spends on your products per site visit) so the site that has the higher average purchase size wins.
In many cases, A/B testing is included in the software you are using. But in case it’s not, or in case you want to understand the math behind the scenes, this article goes through how A/B testing works.
Let’s say you work for an ecommerce company that is trying to improve its average purchase size for online sales. To accomplish this task, your company has built two different improved websites; you’ve now been tasked with determining a data-driven answer in terms of which of the two websites is superior from the standpoint of average purchase size.
Step 1: Collect Data
You monitor each of the two candidate sites for one month and collect data on the purchase amount of 100 randomly-selected purchases each day for each site. You end up with 3,100 samples from each site; the first site sees $128,000 of total purchases, while the second sees $117,000 of total purchases. This translates to an average purchase of $41.29 for the first site and $37.74 for the second. Furthermore, let’s suppose that the first site sees a standard deviation of $22 within the sample of data you collected for it while the second site sees a standard deviation of $21 within its sample.
Step 2: Choosing A Test
From the measured average purchase of the two sites, you cannot necessarily conclude that the first site is the better option, even though its average purchase price is almost $4 higher than the second site. Instead, you need to use a hypothesis test to determine the level of confidence with which you can conclude that. Choosing a statistical test to determine this level of confidence can sometimes be the most difficult part of a statistical analysis! Different test statistics (T, Z, F, etc.) are used for different types of data. Use the Statistics Cheat Sheet for Dummies chart or other related sites like StatTrek to help you choose the right test based on your sample. In this case, since you are trying to test whether one sample mean is higher than a different sample mean (specifically, whether the mean purchase size of the first site is higher than that of the second site) and you don’t know the population standard deviations (these would only be accessible to you if you had measured the size of every single purchase between the two sites, not just a sample of them), the correct test is the Difference of Two Means test with a T-test statistic.

Step 3: Pick A Confidence Level
Almost everyone chooses 95%. If you choose less than that, people may look at you funny or like you have something to hide! Of course there may be appropriate uses for confidence levels less than 95% but it’s not common. If you’re testing something super important, like the safety of airplane parts, you want a confidence level much higher than 95%! Probably like 99.99999% or more! In this case, we’ll stick with 95%.
Step 4: Null And Alternative Hypotheses
In this case you should use a single-tailed T-test because you believe at this point that specifically the first site is outperforming specifically the second, as opposed to simply believing that one or the other of the sites is outperforming the other; a two-tailed T-test would be more appropriate if you are trying to determine whether the average purchase size of the two sites is merely different, not that one is strictly greater than the other. Thus, you can define the null hypothesis and alternate hypothesis like this:
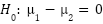
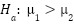
Step 5: Calculating The T-Score
You now have the following figures:
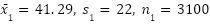
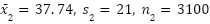
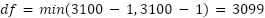
which means:
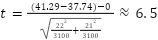
Step 6: Calculating The P-Value
The T-score is very high, which means it’s highly likely that you have enough evidence to reject the null hypothesis and conclude with an extremely high level of confidence (well above 95%) that the first site is outperforming the second. In fact, you have so many degrees of freedom in this test, most T tables won’t even show the exact confidence level that you can have in your conclusion. However, a p-value calculator shows that with as many degrees of freedom as there are in a single-tailed T-test like this one, a T-score of about 1.65 or higher would be sufficient to reject the null hypothesis at the 95% confidence level. In other words, any T-score of 1.65 or higher shows that the first sample mean is far enough above the second sample mean, given how volatile the individual measurements are in relation to those means (indicated by the sample standard deviations) as well as the size of each sample, to conclude with at least 95% certainty that the first site is in fact superior.
If your organization is struggling to implement or interpret tests like these, contact us.
<< Previous Post
"What Is Python, And Why Is It Awesome?"
Next Post >>
"How B2B organizations can use their data"


